13th-century graph traversal
On medieval DAGs, Git, and slop.
Over the past week or so I've taken some time to revisit Ayelet Even-Ezra's Lines of Thought, a study of scholastic practices in medieval Europe. Core to the book is Even-Ezra's thesis that medieval scholars made regular use of what she calls horizontal trees (HTs), a particular kind of tree-like diagram. Even-Ezra highlights a wide variety of domains where medieval scholars used these HTs, including text summarization, analysis of poetry, and grammar.
Far from being simple diagrams, Even-Ezra argues that users of these HTs followed a particular set of rules when writing and reading them. HTs started from the left and proceeded rightward, with each node in the graph representing some concept or sentence fragment. Following nodes from left to right generally produces a complete Latin sentence or answer to some question, implying the HTs were meant to be read in a specific fashion.
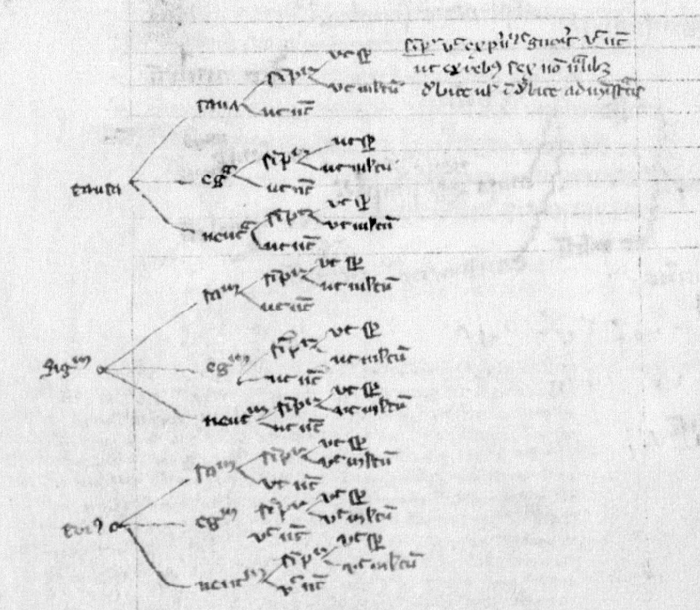
A reader with some mathematical training will notice that despite some minor differences in terminology from what one might see in graph theory - a graph walk becomes an HT trail and a leaf node becomes an HT terminal node, for example - Even-Ezra effectively describes the medieval use of directed acyclic graphs (DAGs) in scholarly life. One of the domains where this shows through most strongly is the ars dictaminis, or art of letter-writing, as exemplified in Lawrence of Aquilegia's works.
A scholar from the late 13th century, Lawrence is perhaps best known for his Practica sive usus dictaminis, a work designed to assist in the writing of letters. The bulk of this work is a series of tabulae, or graphs designed for the automated generation of letters. Each graph corresponds to a particular portion of a medieval letter, such as the salutation or petition. By executing a particular walk of a graph, the writer would produce a legible letter section; by executing a walk of all graphs, they would produce a legible letter in its entirety. Lawrence, in effect, gave his readers the ability to create letters (or at least documents resembling letters) with no more than the ability to write and follow a series of HTs. In doing so, his work had a secondary effect on the act of writing, turning the writer of a letter using the Practica into a sort of automaton while assigning a greater sense of authorship to the one who wrote the input HTs to the letter-writing machine1.

While most other forms of HTs produced a single sentence for a given walk, the tabulae are a particularly powerful example of their algorithmic, generative power. Where Ramon Llull's Ars inspired modern combinatoric thinking, Lawrence's Practica preceded modern ideas of graphical thinking and data compression. When writing and copying its graphs, its authors did not do so from whole cloth. Rather, they combined sets of other letters available to them in summarized form. These graphs represented not just a method for writing letters, but the collective memory of a group of authors compressed into a smaller set of what one might call data structures today. The resulting structures contained less information than the original corpus of letters - it is not possible to reliably reconstruct a document with the tables of the Practica - but the process of constructing the graphs allowed an author to represent the idea of a set of letters, as well as the means to generate new ones.
Key to the success of the Practica was its ease of use in combination with its ease of modification. Its graphs were not fixed objects, but rather dynamic instruments that an author could shape as needed to fit their circumstances. Making a copy of the tabulae, then, meant copying the original author's interpretation of a prior corpus of letters alongside one's own ideas of what was important for some given place and time.
Such notions of authorship and graph representations of text remain with us today in modern computing. A given software project may contain the contributions of thousands of contributors over many years, building up a corpus of knowledge in files not too unlike the folios of Lawrence's era. Contributors frequently revise these files, whether by adding or deleting them outright, rearranging the contents to make some assertion true, or simply making aesthetic changes. This poses a challenge for the parties maintaining such a project; the collective memory of the authors is valuable, but storing a complete copy of the project for every change may be impractical. (As of this writing, the Linux kernel project has over 1.3 million revisions2.)
The solution to this problem is, as it was in the 13th century, to use graphs. Git, for example, is a program that is in effect the de facto standard for version control in software projects today. It is popular at least in part because it does not store source code directly. Instead, it stores a repository of project revisions as a directed graph starting from some beginning state, with each node containing some set of changes to the project. This graph can (and does) split into branches and merge much the same way as a medieval HT or a copy of the Practica. To produce a valid copy of source code at some point, one must walk the graph from the beginning and apply each revision in order until arriving at the desired node. The resulting product is source code rather than an announcement about the election of a bishop, but the process for producing it is largely the same.
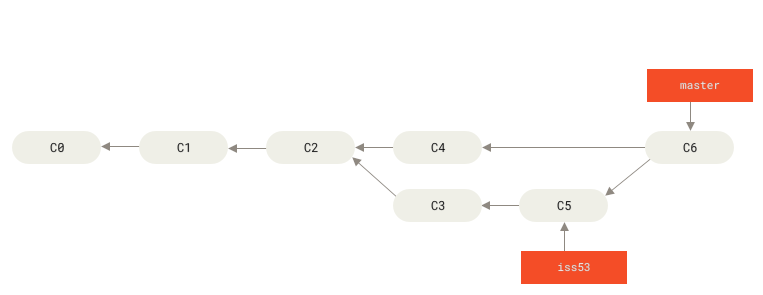
As with the Practica, the contents of a software project do not exist outright in a Git repository. Only the process for generating them exists, as does the input graph for that process. Unlike the Practica, however, every node in a Git repository graph represents a complete revision of the project. Walking from the beginning of time to a node in a graph produces a faithful reproduction of an author's copy of the project at some point in time. This is not a guarantee the Practica can provide, nor is it something it is designed to do.
Beyond a view of the Practica as some ancestor of modern version control, it may be more accurate to say that it presaged another facet of modern computing life: Slop. Lawrence promised users of his method the ability to generate letters with no regard for the content therein, and with no more skill required than the ability to write characters on parchment. Large language models (LLMs) offer a similar appeal in the 21st century. To build a model, an automated training process ingests a corpus of data, decomposing its contents into high-dimensional vectors and data structures designed to predict output given some input. While the structures this training process produces look very different from those of the Practica, a user engages with them in much the same way, though the computer does the majority of the work of text generation.
Much like their medieval counterparts, LLMs erase authorship in favor of a looser, compressed model of a body of works, allowing one to generate texts that feel like they came from the model's originating corpus, though the result may be a text that never existed or that may not make sense at all. There is a crucial difference, however. The Practica promised its users not just the ability to automatically generate text, but to amend the model and interpret it to suit various needs as they arose. LLMs provide no such allowance. An LLM's underlying model is not something that a user can easily modify or amend to fit their own needs; it instead sets the boundaries of the semantic space in which the user is allowed to operate.
Modern software version control and large language models then represent two divergent paths from where Lawrence started. Where one refines and automates the idea of collective authorship, the other destroys it. Compression of knowledge is never a neutral act; the same processes to facilitate reproduction of works can also be used to annihilate their understanding.
- Even-Ezra, A. Lines of Thought. p134
- https://github.com/torvalds/linux/
- https://git-scm.com/book/en/v2/Git-Branching-Basic-Branching-and-Merging